If you had been to university and attended a 3rd year physics course, I guess you would have stumbled over these 4 neat equations. For those of you who do not know them, they are Maxwell's equations (with the help of some other geniuses like Faraday, Gauss and Ampere). They look so simple, and are too (if you know the mathematics behind them). That is what makes them so beautiful. In four simple equations, one can in principle describe the whole of electrodynamics.

If you ever went through school and university, spending the better part of 16 years behind books studying, and then - after years and years of lectures on electrostatics, magnetism and optics - one day, the lecturer stops after having derived these four equations, you could begin hoping to understand the impact this had on me.

The day Professor Moraal from PU for CHE derived Maxwell's equations in front of me, I was totally stunned. 16 years worth of information contained in 4 equations so simple anyone can understand them (mathematically, not necessarily scientifically). They describe the electrical and magnetical fields in free space, and in essence contains everything you need to know to calculate the behavior of an electromagnetic field in free space.

Okay I must confess, they might look deceivingly simple, but they are not really. The amount of information they contain is stunning. The amount of scientific processes and value they contain can be partly comprehended if you take into consideration that they describe the whole of electrodynamics - a field where electrostatics, magnetism and optics are combined into one cohesive concept.

But it does not stop at these equations. They are only an illustration of something bigger. Maybe another example of mathematics that amazed me was the proof of the very well known Power Theorem - used by most high school and university students:

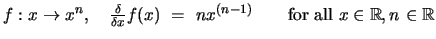
Well, like all things in the world of mathematics, each and every formula and theorem needs to have a valid proof. This one - used unquestioningly and without any further consent by so many people - is no different. It too has a proof. But it is the proof that caught my attention even in my first year on university.

In order to prove that theorem, we need to make some assumptions on the nature of n and x. Lets assume for now that we want this to be valid for all x in the real domain, and all n also in the real domain. This has some interesting consequences. Let us simplify the problem and divide it into several smaller problems. First, we try to prove it for all n > 0 in the integer domain. Secondly, we need to prove it for n = 0. Thirdly, for n < 0 in the integer domain. Fourthly, for n any number in the rational domain. And lastly, for n any number in the irrational domain. If we have proven this, then we can assume the theorem valid for all n in the real domain, as stated in the theorem.

I cannot remember the whole proof as I did this several years ago, but I do remember the essentials behind it. The first subproblem can be proven using mathematical induction and the Binomial Theorem. The second by using the definition of a derivative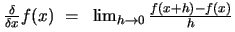

, the third by using the differentiation methods for power functions after applying the reciprocal rule, the fourth by using the chain rule for differentiation and power function differentiation and the fifth by using logarithmic differentiation. Where does Pi fit into this discussion? Well, one of the most astonishing results I think ever obtained was the unification of optics with electromagnetism by James Clerk Maxwell. His wave equations predicted that the speed of light should be given by

, and it was found to be surprisingly accurate. This was no coincidence as there are indeed relationships between c, μ₀ and ε₀. c is the speed of light in a vacuum. μ₀ is the magnetic permeability of free space and is given by μ₀ = 4π10^-7. ε₀ is the electrical permittivity of free space and is given by ε₀ = 8.854187817 * 10^-7. As you can see, the value of Pi is present in the definition of μ₀. So too is it present in Coulomb's Law, contained together with ε₀ in the constant that relates the electric field with the charge divided by the square of the distance from the particle. The interesting thing is that Pi is observed in equations and mathematics that describes electrostatics, so too for magnetism, and also in optics. It almost seems as if Pi is the number that ties all these fields together as can be seen by the Maxwell equations as well. But this irrational number is the relationship between the circumference of a circle divided by its diameter! That has got nothing to do with electrodynamics, or does it? How is it that this irrational number appears in each and every branch of physics? When this number is defined as mentioned above? That is why Pi is so special to me. Nobody can explain why this number has the properties I mentioned.

So what is the big deal you may ask? The big deal is that in order to prove something like the Power Rule, such a diverse set of methods are used to prove the same theorem but for different domains. This shows the cohesion of mathematics - the intrinsic consistency and correctness of what we call "mathematics". Maxwell's equations shows how proper and perfect mathematics is for describing scientific phenomena, and how structured and logical physics is. Pi illustrates the coupling between mathematics and physics and reality. Mathematics was not invented, it was created by God and discovered by man. Because it is something too perfect to have been of human origin.