I must confess - although I had a fairly extensive education in higher mathematics, I am by no means a mathematician. I do love maths with a passion though, so when I played some Putt-putt with my kid the other day, it was just logical that I would use it as a means to teach her some algebra and basic trigonometry.

I started out with a puzzle that I wanted her to solve. The specific problem was not too straight forward for a 4th grader to solve. We were at one of the holes resembling the shape below.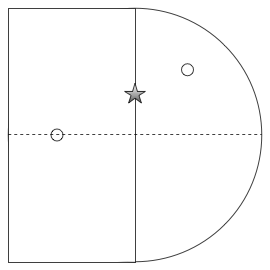

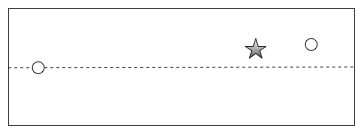
I wanted her to tell me where on the perimeter of the circular section of the course she needed to hit the ball to get it in the hole. Assuming that there is some obstruction between the ball and the hole, that the starting position is fixed, and that the horizontal distance between the ball and the centre of the semicircle is less than the horizontal distance between the centre of the semicircle and the hole (to the right of the obstruction in the sketch). This clearly is too advanced to start out with, so I started with a simpler problem resembling one of the other holes we visited.

Once again, the question was, where to hit the ball to bounce it off the side around the obstruction into the hole on the right hand side. But to get to that solution, I had to teach her a lot about linear equations, solving basic algebraic equations, plotting lines on the cartesian coordinate system, slopes, intercepts and determining the formula of a line based on given points.

There are two ways I know of to solve the problem. One is by determining the solution to two linear equations, the other by using basic trigonometry. I will show both approaches here.

Problem Statement - Intermediate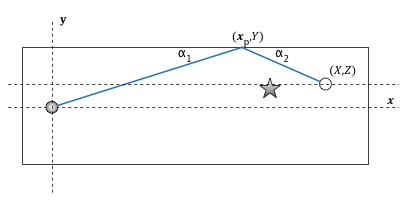

I have arbitrarily placed the origin of the cartesian axis over the ball, therefore fixing its location at (0,0). The angle of incidence of the ball is α₁, and the angle of deflection is α₂. The point where the ball reflects off the wall of the Putt-putt course is (x_p,Y). The hole is located at (X,Z).

The unknown we need to solve for is x_p, as all other variables can be calculated / measured. Some assumptions:

1. No friction
2. No drag
3. Perfectly flat surfaces
4. Perfectly inelastic collisions
5. Speed of ball is not important, only the angle of deflection.
6. The obstruction is large enough that a direct line between the ball and hole is not possible, but small enough not to interfere with any bounced lines.

Algebraic Approach
Let the line describing the incidence segment be known as line a. Let the line describing the deflection segment be known as b. Then it follows from the definition of a line that:

Trignometric Approach
We define two triangles :

---

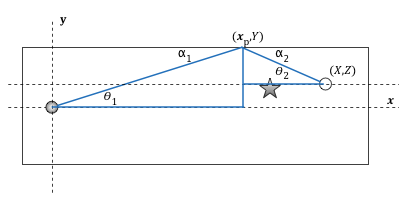
Problem Statement - Advanced

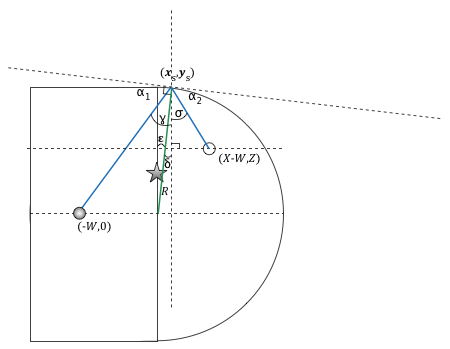
This is the same problem in essence as the intermediate situation, however the non linear characteristic of the circular section complicates things. Looking at the physics, it is clear that at the point on the circumference where the ball would bounce off against, we can draw a tangent line and the angle of incidence would equal the angle of deflection relative to that tangent line. The problem is that the tangent line has a different angle at every point on the circumference, thereby making the calculation much harder.

The unknowns we need to solve for are x_s and y_s, as all other variables can be calculated / measured. Some assumptions:

1. No friction
2. No drag
3. Perfectly round surfaces
4. Perfectly inelastic collisions
5. Speed of ball is not important, only the angle of deflection.
6. The obstruction is large enough that a direct line between the ball and hole is not possible, but small enough not to interfere with any bounced lines.
7. The distance W is smaller than the the distance X-W, meaning the x-component of the hole is further from the circle's centre than the ball is from the centre. This assures that the ball has to bounce off the circle and not off the flat section.

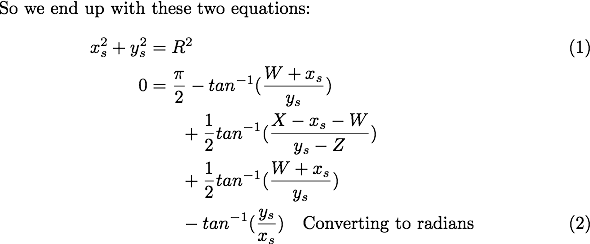
My math is not good enough to know how to solve these two equations symbolically. However an easy way to solve them is to plot both for a given set of course dimensions, and see where they intersect.

Let:
R = 10
X = 7
Z = 7
W = 3

Then:

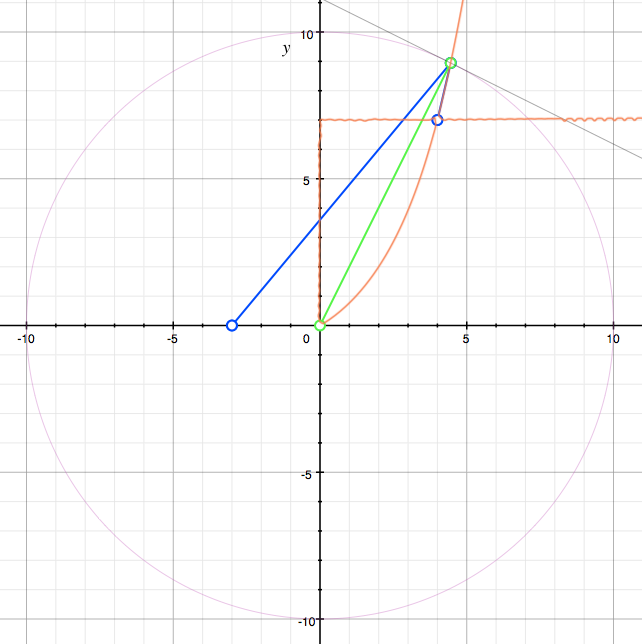
The pink circle (equation 1) and the orange graph (representing equation 2) intersect at two locations. The part where equation 2 approximates y = 7 is not a real solution, only the part that looks like a half parabola is. This curve intersects with the circle at the point

The blue line represents the ball's trajectory. The green line represents the radius of the circle. It is clear from this that the angle of incidence is equal to the angle of deflection at the tangent through the point in our solution. Our solution seems to be correct. Simply measure off this distance on the course and you will be able to hit a perfect hole in one - provided of course your aim is any good.